The Step Model geometrically displays the critical measures and rotation points needed for the creation of realistic footfall patterns.

It exactly defines foot placement, not the real movement of any body segment during a step, and organizes the distance and direction relationships for the 4 minimum points of gait and foot-line, at the instant of heel-contact.

Each Step Model defines a 2D step-plane. The orientation of this plane is arbitrary. Sequential planes are related since the step-heel-point in the current plane is the same as the start-heel-point in the next.

Direction changes during a step are described by 4 of the fundamental parameters:
1) aberrations
2) push-off angle
3) and 4) foot angle and foot offset.

They are all accounted for by rotating the whole model, then aligning the appropriate heel-point. The side-step nature of foot offset is built into the model, and doesn't need extra treatment. If there's an aberration, the whole model is rotated for the rotation part, and then the model's start heel-point aligned with the end heel-point of the aberration.

The circle for the head (COM, more or less) doesn't represent the real position of the head, it's just to help visualize. And, hip joint architecture may introduce a minor variation in the step-out arc characteristics, but that's left off for now.

2. The Standard Model

These are the values for the standard model, and are the minimum number of measurements needed.
Step-out-line = 15”
Pelvic stretch = 0"
Rear-leg-line = 15”
Straddle-line = 8”

Unfortunately, literature walking base measurements can't be used to estimate straddle-line. Walking base changes with angular changes in the body DOT (even if walking straight), but straddle-line doesn’t, so the two aren’t comparable, even though they're related. Walking straddle is walking base, but measured at the heel-points instead of the point of contact of the heel. For str8, Wstr varies as shown below.

Walking Straddle
L15{0}[15] str8 and R15{0}[[15] str8	8.00	- walking straight, no turns, walking straddle (Wstr) = straddle-line (str)
L15{0}[15]str8:L10R and R15{0}[15]str8:R10L	10.57	- walking straight, both feet 10 deg internal turns, Wstr > str
L15{0}[15] str8:L10L and R15{0}[15]str8:R10R	5.35	- walking straight, both feet 10 deg external turns, Wstr < str

For the standard model, I also include the foot models to make analyzing the plot more intuitive, but it isn’t required. I could just as easily be using a dot or cross, since the heel point position is the only thing that matters for distance and direction. But adding the foot model is very easy to do and gives a much more realistic graphic representation. It also makes it possible to see body DOT relationships, and much easier to see plotting errors, distance relationships, and characteristics derived from plot overlays.

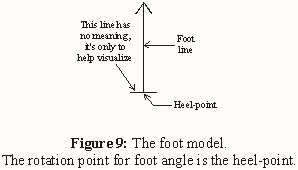
Foot model length = 8”, measured from the heel-point (which is the rotation point for foot angle) to the tip of the toe, along the foot-line. The horizontal line is 2” and is only to help visualize.

Gray step-foot models represent footprints, and black reference-foot models indicate a foot in the air, or some other standard reference.

When the straight foot angle is 0 deg, so there's no push-off angle, as in all the plots so far, the step-foot-line is parallel to the rear-leg-line of the other foot's next step.

Group the horizontal line and foot-line, and change the rotation point to the heel-point.

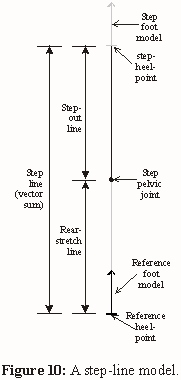
Group the step-out-line and the step-foot model and change the rotation point to the bottom of the step-out-line (The rotation point for foot offset is the step-pelvic joint, which is the bottom of the step-out-line.). Then group this figure with the rear-stretch-line and reference-foot model.

Complete the figure as shown in Fig.10.

Group the whole thing after it’s built.

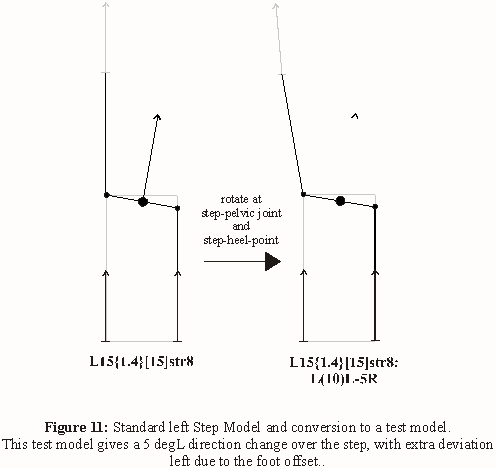
3. Test Step Model

When applied to real data, each step would have a unique model constructed from the data points.

For standard plots, though, it's easier to have just one. Luckily, the left and right steps can be put into one, even if each has different step-out and rear-leg lines, as well as independent foot angles and offsets, push-off angle and aberrations. As long as the straddle-lines are the same, which means the same pelvic-stretch.

If the notation for a Step Model has no reference to the other foot, it's for only one step. Eg. L15{0}[15]str8:L(5)R-10R shows only the parameters for the left step. In this model, the right step-line has no foot angle or offset, is dimensioned the same as the left, and is only to help visualize. L15{0}[15]R15{0}[15]str8:L10L represents both steps, with only the left showing a direction change.

So far, I've kept the straddle-line constant in all plots, and include both steps on a single model.

Foot offset / Leg angle Calculations:

The linear value of foot offset is difficult to use, though it may be easier to visualize. Luckily, this can be converted to leg angle, if the step-out-line is known.

At the instant of heel-contact, if you could freeze yourself in space, just before you plant the front foot, you could move the foot from side to side, and, with constant step-out-line, its path would describe an arc, the step-out-arc.

Step-out-line = radius of the step-out-arc = r = 15”

If you could spin your leg all the way around, the step-out-line would be the radius of a circle,. Since r is known, the circumference of the circle can be calculated.

circumference of step-out-circle = 2 (pi) r

=2 (3.14)15.0”

=94.2”

and,

360.0 deg leg angle / 94.2" foot offset

= 3.82 deg leg angle / " foot offset

or,

0.26” foot offset / deg leg angle

So, if the foot moves 1” along the arc, that’s a leg angle of 3.82 deg, and a leg angle of 1 deg is a 0.26" (along the arc) foot offset. It's much easier to refer to foot offset as deg leg angle, eg. (10)L.

Changes to the standard model change it's overall dimensions, making it more difficult to accurately place (if you want to also use a stationary line or point as a reference), so set up a standard page with the standard step model already positioned on the start. Somewhere on the page, add a blank table to record the distance values from the dimension lines, and a box with the line description of the sample Step Model values.

When changes to the standard model are complete, copy and paste, and leave the copy on the other side of the page for posterity.

For L(3)L-2L:R5R (this person would have equal left and right stride measurements, but the path would have an extra shift left at every left step):

Select the standard Step Model and ungroup.
Select the left step-out-line/foot model and rotate 3 deg CCW.
Ungroup the left step-out-line/foot model, then select the left step-foot model.
Rotate 2 deg CCW.
Select the right step-out-line/foot model and ungroup.
Select the right step-foot model and rotate 5 deg CW.
Select entire figure, then group.
Copy and paste, then move the copy to the other side of the page. This one is kept on the page as an example of the sample model, in case there are errors.

That’s all there is to it, you’re ready to plot. The model is already positioned correctly at the start if you used the standard page.

Foot offset is built into the model. Foot, push-off and leg angle rotations are done when plotting.

4. Creating Footfall Plots

Start with the standard page and modify the standard Step Model.
Copy and paste the test Step Model and move the copy off the original to keep.
Copy and paste the test model again. This will be for the first left step.
Move the copy off the original, and rotate for the left foot offset and angle and push-off angle. For L(3)L-2L:R5R, rotate 5 deg CCW.
Align the left start-heel-point on the copy with the left step-heel-point of the last model.
Copy and paste this model, then move the copy off the original.
Rotate the copy for right foot angles, offsets etc., 5 deg CW, then align the right start-heel-point with the last model's right step-heel-point.
Copy, paste, and move the copy off the original and rotate, etc., for as many steps as you like.
Copy and paste the entire path figure with models, and move to a reference page. Make sure to keep its line description with it. Footfall patterns look alike without the descriptions.
Go back and select the first model. By ungrouping and deselecting lines and points, you can drop any reference figures you want. For the first, I drop the step-foot model (the left), start-foot model, trunk direction, pelvis-line and head dot. Delete the rest of the figure.
Select the next model. Ungroup and deselect the reference-foot model (for right step and carry measures), the step-foot model, trunk direction, pelvis line and head dot. Delete the rest of the figure.
Select the next model. Ungroup and deselect the step-foot model, reference-foot model (for left step and carry measures), trunk direction, pelvis-line and head dot. Delete the rest of the figure.
Select the next model. From here on, drop the trunk direction, pelvis-line and head dot, and the foot model of interest. (The right for this one, left for the next, etc.) For recreating a real path, the reference-foot models would be dropped for every step as well, not just the first two. Also, other reference points and/or lines can be added to the original model and dropped at each step.
Continue until you get tired of it.

I use 7 models, including the first one. This is to help recognize plotting error. For example, if the right strides aren't the same length, there's been an error. Theoretically, they should be identical.

Throughout the entire sequence, "outside" points or lines can be dropped to see the variations in these factors.

Plots can be made with any number of steps to see even broader patterns, if desired, or a different type of test Step Model for each step. Because the start footfall position is always known, any type of Step Model could be inserted into the pathway, as long as it starts at the proper orientation. This is one of the many advantages of this method.

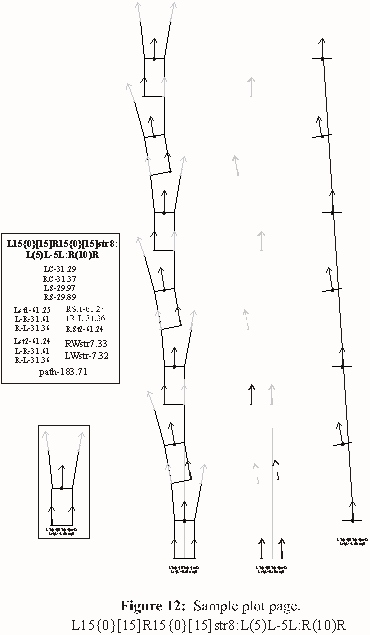
The black footfalls represent a foot in the air at the reference position, and are used to define the left and right carry measurements.

Dimensioning yields the distances between relevant heel-points. A table such as the one below is the result.

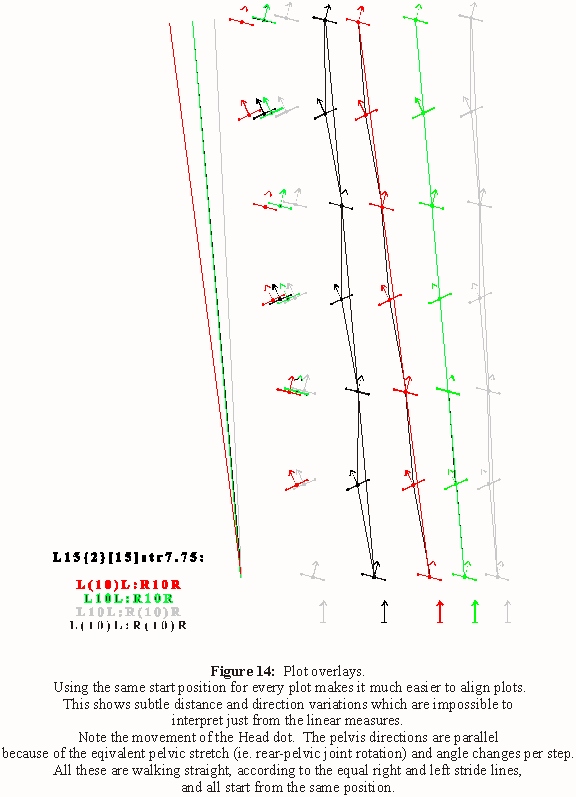
To manipulate the path, select all the footfalls in a plot then group. Since the start footfall is identical for all the plots, they can be overlaid to show subtle elements of path deviation impossible to see otherwise.

Previous Next

Limb & Eye Dominance Techniques Gaits Awareness